Lightweight Reinforcement Learning by Evolving Binary Networks

Binary neural networks can gather hundreds of thousands of frames of training data per second on a single CPU, and evolutionary algorithms make training these nondifferentiable models possible.

This neural network is 600 bytes and runs at 500,000 forward passes per second on my laptop’s CPU.

Heads up: this post has some long equations which don't display well on narrow displays. You might want to switch to landscape mode or a different device to view the equations properly.

Today, reinforcement learning is slow and expensive. Poor sample efficiency, stemming from issues like high-variance gradient estimates and the difficulty of credit assignment, means that agents can require years of experience in an environment to match human performance.

As a result, gathering experience is a key computational bottleneck in reinforcement learning. For each frame of experience, we must run a forward pass through the model. In real-world problems, this leads to large, expensive, and energy-inefficient systems for generating rollouts—OpenAI Five used 128,000 CPU cores for gathering experience in the environment and running evaluation, and 256 GPUs for optimization .

Because inference is such a important part of RL, efficiency improvements to the forward pass directly translate to RL models that are easier, faster, and cheaper to train. In this project, I combine binary neural networks, which are very fast but not differentiable, with evolution strategies, a type of gradient-free optimizer that neatly sidesteps the difficulties of training binary models while offering its own advantages for reinforcement learning.

Binary Neural Networks

Binary neural networks have weights and activations constrained to values +1 or -1.Research in this field has explored a bunch of variants, such as just binarizing the weights, or scaling activations by a learned constant. XNOR-Net is a good paper for getting an overview of this kind of work. Each layer uses the sign function as its activation and computes the function \(f(x; W, b) = \text{sign}(Wx + b)\), where \(x\) is a binary vector of inputs, \(W\) is a binary matrix of weights, and \(b\) is a vector of integer biases.

The weights, inputs, and outputs of a layer are binary in the sense of having two possible values, ±1, but to run the model on standard computing hardware we encode them as the more familiar 0/1 binary numbers by representing -1 as 0 (and 1 as itself). With this encoding, we can fit an entire 64-vector into a single 64-bit quadword. SIMD instructions can operate very efficiently on “packed” vectors of this kind.

The XNOR Trick

There’s a clever trick that enables much faster and more power-efficient neural networks by performing almost all of the required computation with bitwise operations. Let’s say we want to take the dot product of two \(N\)-bit binary vectors, \(\vec{a} \cdot \vec{b} = \sum_i^N a_i b_i\). Since each \(a_i\) and \(b_i\) are ±1, their product is 1 if \(a_i = b_i\) and -1 otherwise. So the dot product is the total count of how many bit places match, minus how many places don’t. Because the two counts must sum to \(N\), we have \(\vec{a} \cdot \vec{b} = 2 \left(\text{# places where a = b}\right) - N\).In notation: $$ \begin{align*} \vec{a} \cdot \vec{b} &= \sum_{i=1}^N a_i b_i \\\\ &= \sum_{i=1}^N \mathbf{1}_{a_i = b_i} + -\mathbf{1}_{a_1 \neq b_i} \\\\ &= \sum_{i=1}^N \mathbf{1}_{a_i = b_i} -\sum_{i=1}^N \mathbf{1}_{a_1 \neq b_i} \\\\ &= 2 \sum_{i=1}^N \mathbf{1}_{a_i = b_i} - N, \end{align*}$$ where $\mathbf{1}$ is an indicator function and the last equality holds because the equality condition partitions the bits.

Since we’re encoding these vectors as 0/1 bit vectors, \(a \text{ XNOR } b\) is precisely 1 where \(a\) matches \(b\) and 0 where it doesn’t, so we can compute the dot product as \(a \cdot b = 2 \text{ popcount}\left(a\text{ XNOR } b\right) - N\). This takes just a few instructions and is very SIMD-friendly. Since matrix multiplication, convolution, and most other important operations for neural networks are made up of dot products, this makes the forward pass of a binary neural network very fast overall.

Training Binary Networks

However, binary neural networks are discrete-valued, which precludes training them with gradient descent and backpropagation. One solution, used by approaches like XNOR-Net , is to train a model with floating-point weights that are binarized during the forward pass.During the backward pass, the gradient of the loss with respect to the binarized weights is computed with standard backpropagation, and that gradient is applied to the floating-point weights as an approximation to the true gradient. You could think of this as the straight-through gradient estimator for a nondifferentiable "binarize layer."

In this project, I took a different approach: training binary neural networks directly, without gradient approximation or backpropagation. To do this, I used evolution strategies, a type of optimizer that does not require gradients.

Evolution Strategies for Binary Neural Networks

Evolution strategies (ES) are a family of derivative-free optimizers that maintain a search distribution: a probability distribution over possible solutions.This section only briefly covers how evolution strategies work at a high level. For dedicated explanations of the theory and popular variants of the algorithm, I recommend the excellent posts by hardmaru and Lilian Weng. ES improves the search distribution over time by repeatedly sampling some candidate solutions, then trying out each candidate to see how well it works, and finally updating the search distribution towards samples that did well. Unlike the typical approach of training neural networks by gradient descent, this does not require backpropagation, so we’re free to use nondifferentiable models like binary neural networks.

ES has a number of other appealing properties in RL . It does not require assigning credit to individual actions, but rather attributes the total reward for an episode directly to the model parameters.I’m not actually so sure this is a good thing. While the authors argue that this helps reduce variance when actions have long-term consequences, I do think there’s plenty of training signal available if we can figure out which actions lead to which consequences. Additionally, by sharing a table of random numbers across multiple worker machines, were able to train ES in a distributed setting while only synchronizing rewards across machines instead of full parameter vectors. This trick makes ES very parallelizable, and when scaled up it can achieve much faster wall-clock times than modern RL algorithms. While this post focuses on single-machine performance, it’s worth noting that distributed RL and efficient inference are a particularly potent combination.

In this project, I used natural evolution strategies , a variant of ES which tries to maximize the expected value of return for samples drawn from the search distribution. To do this, it estimates the natural gradient Intuitively, the natural gradient is like the regular gradient, but where the distance between two points in parameter space is measured by how much they change the resulting probability distribution over solutions. of expected return with respect to the parameters of the search distribution,Note that these are parameters that define the distribution, not parameters of a neural network (which we sample from that distribution). We’ll be taking gradients with respect to $\phi$, the parameters of the search distribution, but our original model parameterized by $\theta$ can still be nondifferentiable. and then performs gradient ascent on these parameters.

A Distribution Over Binary Neural Networks

In this project, the search distribution is a distribution over the weights of binary neural networks. To keep things simple, I modeled each binary weight as an independent Bernoulli random variable. That is, for each weight \(i\) in the binary network we maintain a parameter \(p_i\), the probability of that weight being 1.

To ensure that these probabilities remain valid \(\left(0 \leq p_i \leq 1\right)\) as the parameters are adjusted by the optimization algorithm, I reparameterized them as \(p_i = \sigma(x_i)\), where \(\sigma\) is the sigmoid function and the parameters \(x_i\) may be any real number. I tried a few schemes for initializing these parameters, but in general the best solution was to initialize each \(x_i\) such that every bit is initially 0 or 1 with equal probability.

For the biases, which are integers, I used a factorized Gaussian distribution, with parameters \(\mu_i\) and \(\sigma_i\) for the mean and standard deviation of the \(i\)-th bias. Beware one possible point of confusion: I’m using $\sigma$ for both the sigmoid function and standard deviation parameters. This produces real-valued samples, so I rounded to the nearest integer and used the straight-through gradient estimator (basically, ignoring the rounding operation when computing gradients). I initialized all of the bias means \(\mu_i\) to 0, and the standard deviations \(\sigma_i\) to 1.

So, our binary neural networks will have weights and biases

\[\theta = \left[ w_1, \ldots, w_N, b_1, \ldots, b_M \right],\]

which are sampled from the search distribution. The complete parameter vector defining the search distribution is

\[\phi = \left[ x_1, \ldots, x_N, \mu_1, \ldots, \mu_M, \sigma_1, \ldots, \sigma_M \right],\]

and the probability density for the search distribution is

\(P(\theta \mid \phi) = \left( \prod_{i=1}^N \sigma(x_i)^{w_i} (1 - \sigma(x_i))^{1 - w_i} \right) \left( \prod_{i=1}^M \frac{1}{\sigma_i \sqrt{2 \pi}} \exp \left( -\frac{1}{2} \left( \frac{b_i - \mu_i}{\sigma_i} \right)^2 \right) \right) .\)

Updating the Search Distribution

Natural ES kind of acts like a policy gradient algorithm, except the “policy” is the search distribution, and the “actions” it takes are parameter vectors \(\theta\) for a model we try in the environment. The goal is to maximize the expected value of \(R(\theta)\), a function which accepts the parameters of an agent as input, runs that agent in the environment, and returns the total reward the agent achieved. It performs this maximization by updating \(\phi\) through gradient ascent.

This idea is often called Parameter-exploring Policy Gradients . To perform the update, we’ll write

\[\nabla_\phi \mathbb{E}_{\theta \sim P(\cdot \mid \phi )}\left[R(\theta)\right] = \mathbb{E}_{\theta \sim P(\cdot \mid \phi )}\left[R(\theta ) \nabla_\phi \log P(\theta \mid \phi )\right]\]

using the log-derivative trick, and estimate this expectation with a finite Monte Carlo sample of models from the search distribution. If this looks almost identical to REINFORCE, that’s because it is—the idea of updating a search distribution like this was proposed in the original REINFORCE paper .

Because the search distribution is totally separable, we can compute each parameter gradient separately. So, the gradients we need are the following:

\[\begin{equation} \frac{\partial}{\partial \mu_i} \log \mathcal{N}(b_i \mid \mu_i, \sigma_i) = \frac{b_i - \mu_i}{\sigma_i^2} \end{equation}\] \[\begin{equation} \frac{\partial}{\partial \sigma_i} \log \mathcal{N}(b_i \mid \mu_i, \sigma_i) = \frac{(b_i - \mu_i)^2 - \sigma_i^2}{\sigma_i^3} \end{equation}\] \[\begin{equation} \frac{\partial}{\partial x_i} \log P(w_i \mid x_i) = w_i - \sigma(x_i). \label{eqn:3} \end{equation}\]

The first two are derived in the REINFORCE paper, and I derive \(\eqref{eqn:3}\) in the appendix. As I mentioned above, the biases must be integers, so I round them during the forward pass and use the gradients computed at that point as an approximation to the true gradient.

The Complete Algorithm

In summary, one iteration proceeds as follows:

• Sample a population of binary neural networks, \(\theta_1 \ldots \theta_T\), from \(P( \theta \mid \phi\)).
• Run each agent in the environment using binary encoding and the XNOR trick, and record the total return it achieves, \(R(\theta_i )\).

Estimate the gradient: \( \nabla_\phi \mathbb{E}_{\theta \sim P(\cdot \mid \phi)}[R(\theta)] \approx \) \( \frac{1}{T} \sum_{i=1}^T R(\theta_i) \nabla_\phi \log P(\theta_i \mid \phi) \).

Update \( \phi \) using the estimated gradient, increasing the probability the search distribution assigns to high-performing binary networks.

Results

Fast Learning on Easy Problems

I was consistently surprised by just how fast binary neural networks are in practice. A two-layer, 64-unit-wide binary network clocked in at 500,000 forward passes per second on my laptop’s CPU, 25 times faster than an equivalent model in PyTorch. Training on easy problems like CartPole was quick too—the model at the start of this article trained in under one minute on CPU.

For fast learning, I found it essential to represent the observations from the environment in a good way. This was particularly tricky because the model only accepts binary vectors as input. For CartPole, it was sufficient to put objects’ positions and velocities into one of several “bins,” but making progress on other environments required more careful feature engineering. I also tried training the model from the raw binary encodings of the positions and velocities, but that didn’t work at all.

Failure to Converge on Hard Problems

Let's not let it fly the spaceships quite yet.

However, although this approach made some progress on all of the environments I tried it on, it wasn’t able to completely solve any environment harder than CartPole. Below, I discuss some problems that I think are responsible for this.

Limitations

Variance Collapse

The biggest issue I noticed was that binary weights stop exploring once they learn. When a parameter \(x_i\) grows large, weight \(w_i\) will be the same in almost every sample. As training progresses and the search distribution gains confidence in which bits should be active, the algorithm as a whole stops exploring, and performance stops improving beyond a point.

A histogram of the binary weight logits $x_i$ over time, with later episodes closer. As the search distribution learns, the distribution of weight logits becomes bimodal and most weights in the binary network assume a fixed value.

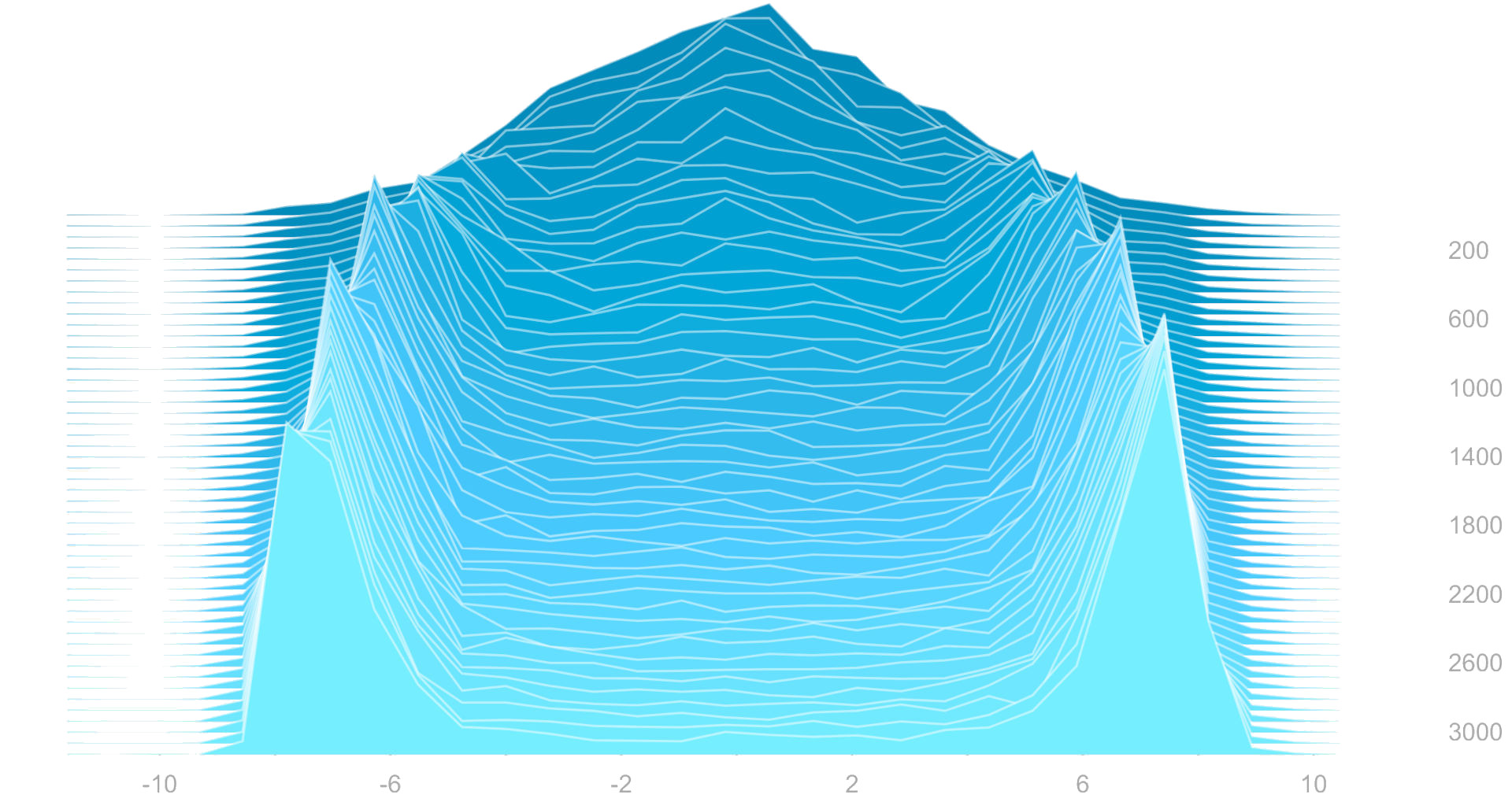
I’ve tried a few things to combat this tendency. Shrinking the bit probabilities towards 0.5 (or equivalently, weight decay on the \(w\) parameters) did a good job extending the time before learning plateaued, as did lowering the learning rate. I also experimented with holding the variance of the bias distribution constant instead of adjusting \(\sigma_i\), similar to OpenAI’s work with ES. Ultimately, though, CartPole was the only environment where the model reliably finished training before it converged to a low-variance regime and stopped learning.

Independence Assumptions

The search distribution I used makes strong independendence assumptions about the network parameters. The parameters definitely aren’t independent, though, leaving information on the table that the search distribution might be able to use to search more efficiently. There are other variants of evolution strategies that do consider covariance between the parameters, such as Covariance Matrix Adaptation ES, but they require second-order information that’s intractible to compute for larger models.

High-Dimensional Search Space

High-dimensional gradients are really amazing. Part of deep learning’s success is that even for models with millions of parameters, the gradient tells each of them how to change and coordinate. Evolution strategies don’t share this scalability, though — they explore parameter space by testing a few random directions around the current solution. This leads to high-variance gradient estimates as the dimensionality of the search space grows.

One reason that ES has seen some success in reinforcement learning is that the true gradient of performance is not available, and must be estimated even for approaches using backpropagation. However, given the success of very large models in other domains, it may be the case that exploring directly in parameter space with ES becomes infeasible for the models required to solve some problems.

Conclusion

For reinforcement learning in challenging environments, massively distributed training across thousands of computers is currently the norm. As we begin to tackle new and harder problems, we can only expect the computational requirements to grow. However, evolution strategies and binary neural networks may provide a more computationally-tractable way of training RL agents.

Building on prior work that investigates scaling ES in a distributed setting , this project takes a complementary approach: improving the efficiency of each experience-gathering agent. I used the derivative-free nature of ES to train binary neural networks without approximating backpropagated gradients. While I’ve only been able to solve easy RL problems with this approach so far, being able to train these tiny, fast neural networks is pretty cool. I’m excited to see what future work that combines this efficiency with ES’s parallelizability could do!