Generating Musical Accompaniment in Latent Space

By predicting the latent code for a whole song given just the melody, we can synthesize drums and bass for any MIDI.

This was the final project for an undergraduate class on deep probabilistic models, and was built with Brendan Hollaway, Anthony Bao, and Hongsen Qin.

Generative machine learning models have famously been used to create new media from scratch, but an even more exciting possibility involves humans collaborating with algorithms throughout the creative process . While generative models are increasingly able to generate convincing images, audio, and text, human input is valuable to choose properties we want the final result to have and to incorporate parts of the human experience we haven’t (yet) been able to train our models to understand.

This project explores co-composing music with a neural network that automatically generates drums and bass for a human-written melody.

Accompaniments generated by our model

Tetris Theme

Generated

Original

Nyan Cat

Generated

Original

In the Hall of the Mountain King

Generated

Original

While this project uses a restricted subset of MIDI (which is itself very restricted relative to all of what’s possible with music), and the samples therefore always sound a little elevator‑music‑y, we believe that this approach would scale well to larger, more sophisticated latent variable models, such as OpenAI’s Jukebox .

Model Overview

Before getting into the details, here’s a brief overview of how the model works at a high level.

The core of the model is MusicVAE , a pretrained model created by Google’s Magenta team. MusicVAE consists of an encoder, which transforms pieces of music into latent variables which capture properties of that music in a simpler compressed form, and a decoder which transforms latent variables back into music. Both the encoder and the decoder are trained on three-track MIDI consisting of melody, drums, and bass, with extra features like time signature changes stripped.As a result, the model doesn’t work very well on music using these features. You might notice this in "In the Hall of the Mountain King" above.

Because we want to generate the accompaniment given a new melody, we train a “surrogate encoder” to mimic the original MusicVAE encoder, while only having access to the melody. Given a dataset of three-track music, we use the MusicVAE encoder to produce a latent representation for each song, then strip out the drums and bass and train the surrogate encoder to predict the latent variables from the melody alone. Finally, given a new melody, we use the surrogate encoder to guess what the latent variables might be for the melody’s (nonexistant!) three-track song, pass those latent variables to the MusicVAE decoder to turn into three-track MIDI, and stitch the original melody back in.

Variational Autoencoders and Latent Space

MusicVAE is a variational autoencoder (or VAE). A full tutorial on VAEs is outside of the scope of this project writeup, but for an introduction I recommend Jaan Altosaar’s tutorial. For the purposes of this project, you can think of a variational autoencoder as a way of representing your data in a simpler and smaller way, as a collection of latent variables. In our case, a MIDI song might take 20 KB to store, but its latent representation is a vector of 512 floating-point numbers, a compression ratio of ten. Despite being much smaller, the latent variables are expected to capture most of the high-level properties of the music, like genre, key, time, and timings for particular events. This is possible because music has patterns that enable it to be described succinctly—you could get a passable reconstruction of some drum parts by just asking a drummer to “play a swing beat.”

Furthermore, latent representations are presumed to live in some “latent space,” about which we make some very strong assumptions. The latent space is expected to be smooth, in the sense that two nearby (512-dimensional) points are expected to represent two songs that sound very similar.The two songs may not have any notes in common, though! Distances and directions are more meaningful in latent space than they are in data space. Directions are often meaningful in latent space; the authors of MusicVAE found that they could move songs in an “add note density” direction to maintain the character of a song but with more notes.

Most importantly, the latent space has a squished and twisted shape (relative to the data’s shape) such that real music appears Gaussian-distributed in this space.This is actually an oversimplification. While ours is Gaussian, VAEs often use other distributions for the latent space. This means that when you sample latent vectors from a Gaussian, they likely correspond to songs that sound reasonable, and conversely real songs frequently map to vectors near the origin. If you were to pick any direction in latent space, find the latent vector corresponding to every popular song and project those vectors onto this direction, then plot a histogram of the resulting values, that histogram should form a standard normal bell curve.

Latent space is very simple (it’s just a multivariate Gaussian), but it’s supposed to represent the full distribution of music, which is complex and multimodal in its common representations (MIDI, MP3, FLAC, etc.). To accomplish this, a variational autoencoder employs two powerful neural networks to translate between data space and latent space. The encoder maps data points into latent variables that represent them, and the decoder maps latent variables back into data space. By randomly sampling points in latent space and pushing them through a good decoder, we can generate endless music, or images, or whatever else the VAE was trained on. What is most remarkable is that variational autoencoders are trained unsupervised. Given a dataset of media, the encoder and decoder learn to create this very special latent space with no additional supervision.

Predicting Latent Variables from a Melody

A lot of the things we want our latent variables to capture—what the song’s genre is, when solos start and end, etc.—are present in all three parts of the original music. When a bass solo starts, the drummer might play a simpler pattern and the melody might stop playing altogether. When it ends, the drummer doesn’t need to know much about the details of the solo to play an appropriate fill. In this sense, the original music is an overcomplete representation, which is why we’re able to compress it so much in the latent space.

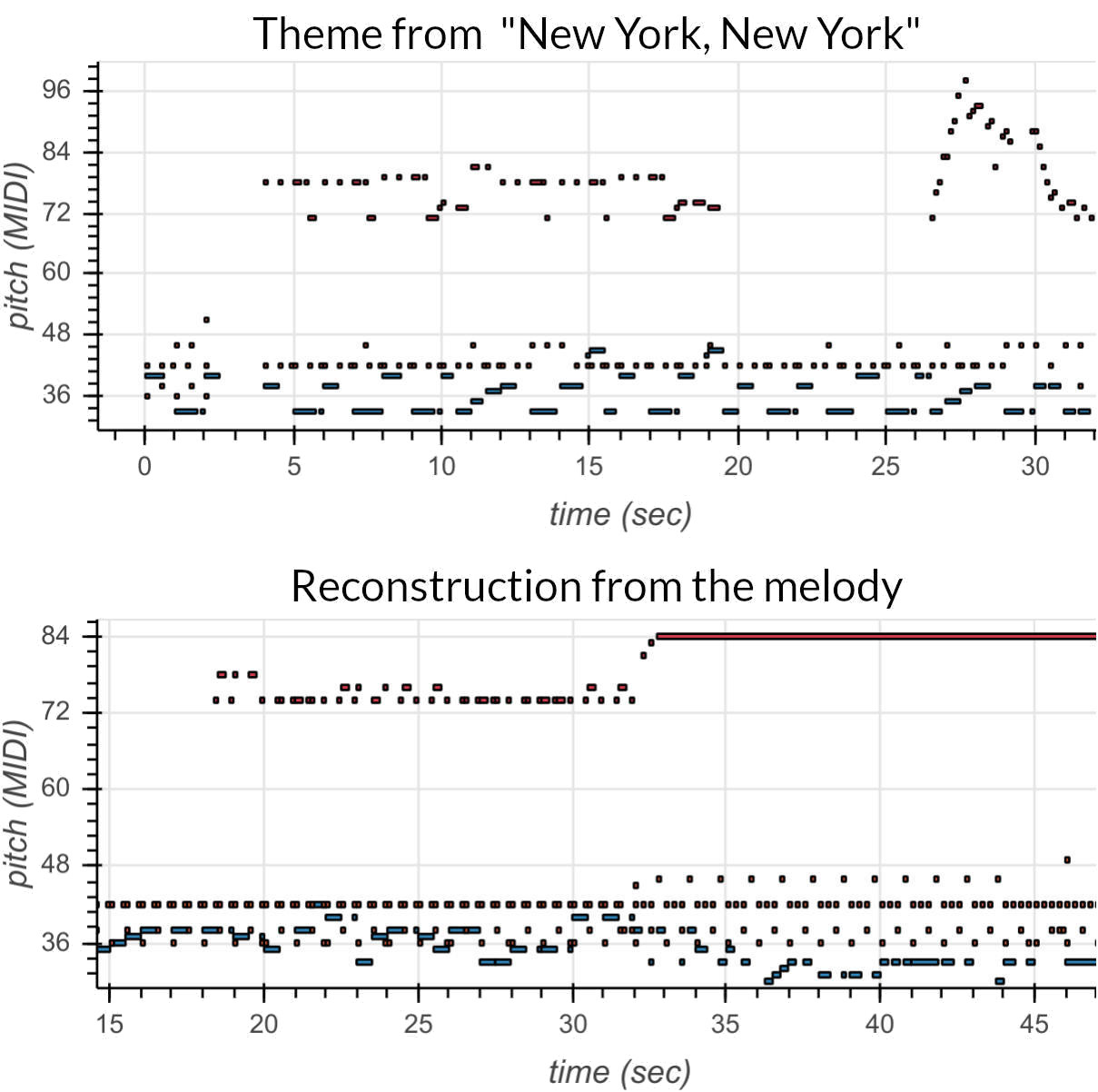
That also means that many properties of a full song’s latent representation can be inferred from just one of the parts. In the plot above, the surrogate encoder and MusicVAE decoder try to reconstruct the theme from “New York, New York” from just Frank Sinatra’s part. Red bars are the melody, blue are the bass, and brown are drums. The model certainly can’t predict the original accompaniment, and it doesn’t even recreate the melody (which the surrogate encoder has access to)—that’s why we stitch the original melody back in as the last step. However, it has correctly inferred a swing beat for the drums, works around important timings in the song, and plays the bass in key. This means that the original MusicVAE encoder learned to encode properties like drum style in the latent space in a simple way, and our surrogate encoder was able to map from the melody to the latent variables that MusicVAE used to represent these properties.

Conclusion

Variational autoencoders have been pretty unpopular recently, due to the dominance of GANs on many of the same generative tasks. However, with some impressive recent results generating high-resolution images and raw audio with more sophisticated VAEs, variational methods are making something of a comeback. Hopefully this post illustrates some of the cool things you can do with an explicit and controllable latent space.

If you like, check out the code and some additional samples on the GitHub repo. And if you find any mistakes, errors, or points of confusion, please let me know!